Vector Reflection

매 프레임당 어떤 물체의 $x, y$에 $vx, vy$를 더해주면 움직임을 만들 수 있습니다. 여기서 $vx,vy$는 $Vector$ 로 바꿀 수도 있는데요, 벡터는 크기와 방향을 가지는 단위이다 라고 정의하며, $( vx, vy \cdots vz )$ 처럼 숫자들로 이루어져 있습니다. 저 숫자 집합에서 크기와 방향을 알아내려면, 피타고라스 정의와 삼각함수를 이용한 계산이 따로 필요합니다. 그래서 단순히 숫자 집합이며 그게 2차원이라면 $(x,y)$, 3차원이라면 $(x,y,z)$를 원소로 갖는 단위$(Class)$라고 이해하는게 편합니다. 프로그래밍이라면 더욱 그렇겠죠.

벡터 연산을 통해 특정 각도에 대한 $vx, vy$의 반사 벡터를 계산 해보겠습니다. (벡터는 영문 대문자 위에 화살표로 표기합니다.ex: $\vec{V}$)

alt text

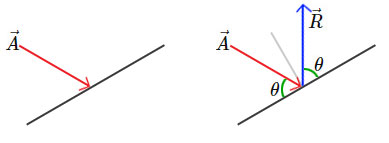
그림과 같이 $\vec{A}$가 반사된 $\vec{R}$을 구하려면 면에 대한 입사각 $\theta$ 를 구해서 $2 \cdot \pi - \theta$로 반사각을 구하고 $\vec{A}$를 반사각 만큼 돌리면 될 것 같은데요, 물론 이런 방법으로도 구할 수 있겠지만, 각도 때문에 삼각함수를 써야 하니 성능이 좋을것 같지 않네요.

alt text

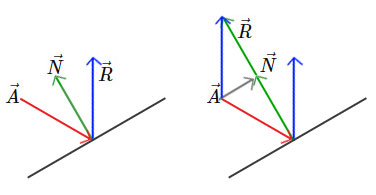
만약 그림처럼 $\vec{N}$을 알 수 있어서, $\vec{A}$에 $\vec{N}$을 두번 빼준다면 $\vec{R}$을 얻을 수 있을것 같은데요. 식으로 표현하면 $\vec{R} = \vec{A} - 2 \cdot \vec{N}$ 가 되겠네요.

그림으로 봐도 $\vec{N}$은 반사된 벽에 수직선인것 같은데요, 벽을 90도 돌리면 될것 같습니다. 우선 벽의 끝 점 $(x1,y1)$에서 시작 점 $(x0,y0)$를 빼 벡터 $(x',y')$으로 만들고, $\theta$ 만큼 돌리기 위해 $\begin{bmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix}$ 를 곱해주면 되는데요, 90도(${\pi \over 2 }$)를 돌려야 하니 $\cos {\pi \over 2} = 0, \sin {\pi \over 2} = 1$ 이 되서 $\begin{bmatrix}0 & -1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix}$ 가 되고, 풀어보면 $(-y, x)$가 됩니다. 이렇게 수직인 벡터를 법선 벡터( normal vector )라고 합니다.

// 벡터 클래스
function Vector2D(x,y){ this.x = x; this.y = y; };

// 벡터 빼기
Vector2D.prototype.sub = function( v )
{
    return new Vector2D( this.x - v.x, this.y - v.y );
}

// 노말( 법선 ) 벡터 구하기
Vector2D.prototype.normal = function()
{
    return new Vector2D( -this.y, this.x );
}

다음은 $\vec{N}$의 길이인데, 벡터의 내적은 $\cos\theta \cdot |\vec{A}| \cdot |\vec{N}|$으로도 쓸 수 있는데요, 여기서 $\vec{N}$의 길이가 1이라면(단위 벡터라면) 계산 결과는 $\vec{A}$에서 법선 벡터로 수직선을 내려 만나는 점까지의 거리가 됩니다. 즉 $\vec{A}$를 $\vec{N}$에 투영한 길이라고 할 수 있습니다. $(|\vec{A}|$는 $\vec{A}$의 길이)

$\vec{N} = \vec{A} \cdot normalize(\vec{N}) \times normalize(\vec{N})$

아래는 벡터의 길이를 구하고 정규화$(normalize)$, 내적, 스칼라 곱을 구하는 함수입니다.

// 길이
Vector2D.prototype.length = function()
{
    return Math.sqrt( this.x * this.x + this.y * this.y );
}

// 정규화
Vector2D.prototype.normalize = function()
{
    var len = this.length();

    return new Vector2D( this.x / len, this.y / len );
}

// 내적
Vector2D.prototype.dot = function( v )
{
    return this.x * v.x + this.y * v.y;
}

// 스칼라 곱
Vector2D.prototype.scale = function( scalar )
{
    return new Vector2D( this.x * scalar, this.y * scalar );
}

$\vec{N}$을 구했으면 이제 $\vec{A}$에서 두번 빼주기만 하면 됩니다.

$\vec{R} = \vec{A} - 2 \times \vec{N}$

벽을 맞고 튕겨나가는 물체의 $(vx, vy)$는 $(\vec{R}.x, \vec{R}.y)$가 됩니다. 아래는 reflection vector 구하는 코드 입니다.

/**
* incidentVec: 입사 벡터
* collisionPlane: 충돌 면( 시작점 Vector2D a와 끝점 Vector2D b 를 가지고 있습니다.)
* return: 반사 벡터
*/
function getReflectionVector( incidentVec, collisionPlane )
{
    var sub =  collisionPlane.b.sub( collisionPlane.a ),    //충돌 면의 벡터를 구하고
        normal = sub.normal(),                              //충돌 면 벡터의 법선 벡터 
        normalized = normal.normalize(),                    //법선 벡터를 정규화
        scalar = incidentVec.dot( normalized ),             //법선 벡터에 투영하여 길이를 구하고
        reflect = normalized.scale( 2 * scalar );           //2 곱하기로 2 * N 벡터를 구함

    return incidentVec.sub( reflect );
};

Canvas example

소스보기