Line Segment
Line Segment
$A\to B$ 라는 선분과 $B\to C$ 라는 선분이 있을 때, 두 선분의 교차 여부를 판단하는 방법에는 여러가지가 있을텐데요, 그중에는 내분점을 이용한 방법도 있습니다. 내분점이란 $A\to B$ 에서 $A, B$ 사이에 있는 점을 말합니다. 무게중심 좌표라고도 할 수 있는데요, $A, B$ 사이의 중점은 $(0.5,0.5)$ 로 $P = A + 0.5\cdot (B-A)$로도 나타낼 수 있습니다. 여기서 $0.5$를 내분점 $s$로 놓고 $(0 <= s <= 1)$을 만족하면 점 $P$는 선분 $AB$ 위에 있다고 볼 수 있습니다. 반대로 $s$가 $0$보다 작거나 $1$보다 크다면 점 $A, B$를 잇는 직선상에는 있지만 $A, B$의 외부에 있다고 할 수 있습니다.
여기서 점 $P$를 선분 $A\to B$와 선분 $C\to D$의 교점이라고 가정하면,
$P = A + s\cdot (B - A)$
$P = C + t\cdot (D - C)$
두 식을 얻을 수 있는데요, $s$와 $t$모두 $( 0 <= (s,t) <= 1 )$을 만족한다면 두 선분은 교차한 상태이며, $s$나 $t$를 이용해 두 식중 하나에 적용하면 점 $P$의 위치까지 계산할 수 있습니다.
위 식을 정리하면
$A + s\cdot (B - A) = C + t\cdot (D - C)$
점$B$에서 점$A$를 빼는건 벡터 $\vec{AB}$라고도 볼 수 있으니
$A + s\cdot \vec{AB} = C + t\cdot \vec{CD}$
한쪽으로 정리하면
$s\cdot \vec{AB} - t\cdot \vec{CD} = C - A$
C - A도 벡터로 계산해서
$s\cdot \vec{AB} - t\cdot \vec{CD} = \vec{AC}$ 로 정리 할 수 있습니다.
여기서 $s\cdot \vec{AB}$는 풀어쓰면
$s\cdot \vec{AB}_x$와
$s\cdot \vec{AB}_y$의 두개의 식이 나와서 계산이 복잡해지기 때문에
$s\cdot \vec{AB} \cdot \vec{AB} - t\cdot \vec{CD} \cdot \vec{AB} = \vec{AC} \cdot \vec{AB}$
양변에 $\vec{AB}$를 내적하여 $\vec{AB} \cdot \vec{AB}$ 를 상수 a로 바꿀 수 있습니다. 벡터 내적의 결과는 scalar값입니다.
미지수가 $s, t$ 두개 있으니 방정식도 두개를 만들기 위해 $\vec{CD}$도 한번더 내적해주면,
$s\cdot \vec{AB} \cdot \vec{AB} - t\cdot \vec{CD} \cdot \vec{AB} = \vec{AC} \cdot \vec{AB}$
$s\cdot \vec{AB} \cdot \vec{CD} - t\cdot \vec{CD} \cdot \vec{CD} = \vec{AC} \cdot \vec{CD}$
로 두개의 식이 나왔습니다. (엄청 복잡해보이네요.)
$\vec{AB} \cdot \vec{AB} \to a$, $\vec{CD} \cdot \vec{AB} \to b$, $\vec{AC} \cdot \vec{AB} \to e$
$\vec{AB} \cdot \vec{CD} \to c$, $\vec{CD} \cdot \vec{CD} \to d$, $\vec{AC} \cdot \vec{CD} \to f$
내적은 최초 점 $A,B,C,D$를 통해 계산이 가능하니 위처럼 상수$(a,b,c,d)$로 바꿔서 정리하면,
$a\cdot s -b\cdot t = e$
$c\cdot s -d\cdot t = f$
흔히 볼 수 있는 연립방정식으로 정리가 되었습니다. 연립방정식 풀이에는 소거법, 대입법등이 있는데, 그중에 행렬을 이용한 크라메르 공식을 이용해서,
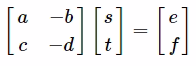 연립 방정식을 행렬곱으로 바꾸고
연립 방정식을 행렬곱으로 바꾸고
$s = { det(M0)\over det(M)}$, $t = { det(M1)\over det(M)}$ 으로 풀 수 있습니다.
$det(M)$은 행렬 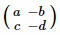 의 행렬식 $( -ad - ( -bc ) )$이며,
의 행렬식 $( -ad - ( -bc ) )$이며,
$det(M0)$은 행렬 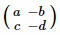 의 0번째 열을
의 0번째 열을 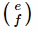 열 벡터로 바꾼
열 벡터로 바꾼 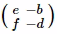 의 행렬식 $( -ed - ( -bf ) )$이고,
의 행렬식 $( -ed - ( -bf ) )$이고,
$det(M1)$은 행렬 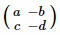 의 1번째 열을
의 1번째 열을 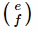 열 벡터로 바꾼
열 벡터로 바꾼 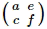 의 행렬식 $( af - ce )$입니다.
의 행렬식 $( af - ce )$입니다.
code
/**
* va -> vb, vc -> vd의 두개 선분 교차점 검색
*/
function detectSegment( va, vb, vc, vd )
{
var AB = vb.sub( va ),
CD = vd.sub( vc );
var a = AB.dot( AB ),
b = c = AB.dot( CD ),
d = CD.dot( CD );
var detM = -a * d + b * c;
if( detM == 0 ) return null; // 행렬식이 없으면 평행하거나, 겹치는 경우.
var AC = vc.sub( va );
var e = AC.dot( AB ),
f = AC.dot( CD );
var s = ( -e * d + b * f ) / detM,
t = ( a * f - c * e ) / detM;
if( s < 0 || s > 1 || t < 0 || t > 1 ) return null;
return AB.scale( s ).add( va );
};