line pixelate

픽셀로 이루어진 디지털 공간에 선을 그리기 위해서는 두 점 사이에서 적절한 픽셀을 선택하는 과정이 필요합니다.

function lineTo( ax, ay, bx, by ) // arguments 모두 int형
{
    //code
}; 

위와 같이 $a$에서 $b$로 선을 그려야 되는 함수가 있을 때, 두점 사이의 픽셀들을 구하는 방법은 3가지 정도로 압축할 수 있습니다.

• 1차 함수

  직선의 방정식을 이용해 선을 그립니다. $(m \neq 0)$ 일 때 $y = mx + b$를 이용해 $x$가 $ax$ 부터 $1$씩 증가하면 그에 맞는 $y$를 구할 수 있습니다. 이때 $y$절편 $b$는 $-m \times ax + ay$가 됩니다.

  $y$의 증가분은 $x$의 증가분 * 기울기$(m = {by-ay\over bx-ax})$와 같기 때문에 $( y - ay ) = m( x - ax )$라는 식을 세울 수 있는데, 이걸 풀어서 $y$로 정리하면 $y = mx - m \times ax + ay$가 됩니다. 여기서 뒷부분 $-m \times ax + ay$는 $b$로 치환할 수 있는 상수 입니다.

  위 식을 간단히 javascript로 정리하면

  var m = (by - ay) / (bx - ax),
      b = -m * ax + ay,
      y;
  
  for( var x = ax; x <= bx; x++ )
  {
      y = m * x + b;
      drawPixel( x, Math.round( y ) );
  }
  

  로 나타낼 수 있습니다. (단 $dy > dx || ax > bx || bx-ax=0$인 경우에 대한 예외처리는 필요합니다. )

• DDA - Digital differential analyzer

  dda 알고리즘은 기울기를 이용합니다. $x$가 1씩 증가할 때 $y$의 $n$번째 위치는 그 전 $y$의 기울기 $m$만큼 더한 값과 같다 라는게 기본 아이디어입니다.

  \(y=y_{n-1}+m\)

  라는 식을 세울 수 있는데요, javascript로 정리하면

  var m = (by - ay) / (bx - ax),
      y = ay;
  
  for( var x = ax; x <= bx; x++ )
  {
      drawPixel( x, Math.round( y ) );
      y += m;
  }
  

  위 식과 비교해서 곱하기 연산이 하나 줄고 $b$를 계산할 필요도 없어졌습니다. 초당 60번씩 몇백개의 선을 그리는 그래픽 라이브러리에서 봤을 땐 꽤 괜찮은 성능향상인 것 같네요.

• Bresenham algorithm

  Bresenham 알고리즘은 $y_{n+1}$의 $y$위치가 이전보다 0.5가 크면 $y = y + 1$, 작으면 $y = y$가 기본 아이디어입니다.

  

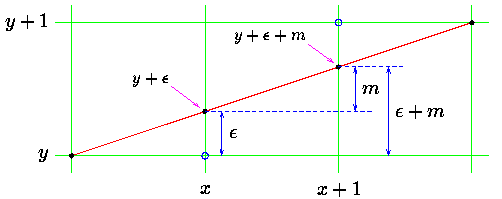
  위 그림처럼 $e$라는 값을 따로 두고, $x$가 증가할 때 마다 $e$도 기울기$(m)$만큼 증가하면서 $e$가 $0.5$보다 커지면 $y$를 $1$증가하는 방법으로 Math.round 연산을 대신 할 수 있는데요, code로 보자면

  var m = (by - ay) / (bx - ax),
      y = ay,
      e = 0;
  
  for( var x = ax; x <= bx; x++ )
  {
      drawPixel( x, y );
  
      e = e + m;
      if( e > 0.5 )
      {
          e = e - 1; // e를 초기화
          y = y + 1; // y 증가
      }
  }
  

  DDA와 비교해서 코드와 연산만 늘어났을 뿐 좋아진 점이 보이지 않네요.

  위 코드에서 $float$ 연산 부분을 모두 $int$ 연산으로 바꿀 수 있다면 성능향상을 기대할 수 있을것 같은데요, $m$은 기울기$({by-ay\over bx-ax})$라 특별한 경우가 아니라면 대부분 실수일테니 $e = e + m$과 $e > 0.5$ 비교 부분을 정수로 바꿔주면 될 것 같습니다.

  $dx = bx - ax$, $dy = by - ay$ 일때,

  $e = e + m$을 $e = e + {dy\over dx}$로 보고 양변에 $dx$를 곱해주면 {${e\cdot dx = (e+{dy\over dx})\cdot dx}$}

  ${e\cdot dx = e\cdot dx + dy}$ 가 됩니다.

  여기서 양변에 나오는 $e\cdot dx$ 를 새로운 $e$인 $e'$으로 놓으면

  $e' = e' + dy$ 라는 식으로 바꿀 수 있습니다.

  두번째로 $e > 0.5$ 부등식 양변에 $2dx$ 를 곱해주면 $e\cdot 2dx > dx$ 로 바꿀 수 있는데, 좌변 $e\cdot 2dx$를 $e'$으로 바꿔주면 $2\cdot e' > dx$ 라는 부등식이 됩니다. $e$의 시작은 $0$이기 때문에 $e'$을 $e$로 둬도 위코드는 변함이 없는데요, 다만 $e = e - 1$부분의 $e$는 $e\cdot dx$로 바꿔줘야 합니다.

  $e = e - 1$ 양변에 $dx$를 곱하면 $e\cdot dx = e\cdot dx - dx \to e' = e' - dx$로 바꿀 수 있습니다.

  javascript code

  var dx = bx - ax,
      dy = by - ay,
      y = ay,
      e = 0;
  
  for( var x = ax; x <= bx; x++ )
  {
      drawPixel( x, y );
  
      e += dx;
      if( ( e << 1 ) > dx ) // 곱하기 2는 비트연산으로 대체 
      {
          e -= dx;    // e를 초기화
          y++;        // y 증가
      }
  }
  

  실제 성능을 비교해 보진 않았지만 bresenham`s line algorithm은 "extremely fast"하다고 하네요.

실제로 선을 그리는 함수를 개발할 일이 많지 않을텐데요, 직선 방정식을 loop내에서 기울기만으로 처리하거나 정수 연산으로 바꿔주는 등의 최적화 과정은 눈여겨 볼 만한 것 같습니다.

Canvas example

위 3가지 방법으로 라인을 그리는 예제입니다.

Lego Clock

소스보기